Link to previous part

ROUGH NOTES (!)
Updated: 28/10/24

Regular points; Manifolds; Tangents and Normals

Back to top.

\[{ \underline{\textbf{Regular points}} }\]

Obs [Implicit function theorem for ${ C ^p }$ maps ${ \mathbb{R} ^n \times \mathbb{R} ^m \to \mathbb{R} ^m }$]:
Let ${ f : U (\subseteq \mathbb{R} ^n \times \mathbb{R} ^m \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^p }$ map. Let ${ (a, b) \in Z _f }$ be such that ${ \partial _2 f (a, b) }$ is nonsingular that is

\[{ \begin{aligned} &\, (a, b) \in U, \\ &\, f _1 (a _1, \ldots, a _n; b _1, \ldots, b _m) = 0, \\ &\, \quad \quad \quad\vdots \\ &\, f _m (a _1, \ldots, a _n; b _1, \ldots, b _m) = 0 \end{aligned} }\]

and

\[{ \det \begin{pmatrix} D _{n+1} f _1 (a, b) &\cdots &D _{n+m} f _1 (a, b) \\ \vdots &\ddots &\vdots \\ D _{n+1} f _m (a, b) &\cdots &D _{n+m} f _m (a, b) \end{pmatrix} \neq 0 . }\]

Then there exist open neighbourhoods

\[{ (a, b) \in \mathscr{U} \subseteq U, \quad a \in \mathscr{V} \subseteq \mathbb{R} ^n }\]

and a ${ C ^p }$ map

\[{ g : \mathscr{V} \longrightarrow \mathbb{R} ^m }\]

such that

\[{ Z _f \cap \mathscr{U} = \lbrace (x, g(x)) : x \in \mathscr{V} \rbrace }\]

that is

\[{ \begin{aligned} &\, Z _f \cap \mathscr{U} \\ = &\, \lbrace (x _1, \ldots, x _n ; g _1 (x _1, \ldots, x _n), \ldots, g _m (x _1, \ldots, x _n)) : (x _1, \ldots, x _n) \in \mathscr{V} \rbrace . \end{aligned} }\]

So informally there are ${ m }$ variables ${ x _{n+1}, \ldots, x _{n+m} }$ that uniquely solve the system of equations

\[{ \begin{aligned} &\, f _1 (x _1, \ldots, x _n; x _{n+1}, \ldots, x _{n+m}) = 0, \\ &\, \quad \quad \quad \vdots \\ &\, f _m (x _1, \ldots, x _n; x _{n+1}, \ldots, x _{n+m}) = 0 \end{aligned} }\]

in a neighbourhood of ${ (a, b) }$ as ${ C ^p }$ functions of the other ${ n }$ variables ${ x _1, \ldots, x _n . }$

Obs [Implicit function theorem for surjective derivative]:
Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^p }$ map. Let ${ x _0 \in Z _f }$ be such that ${ Df(x _0) : \mathbb{R} ^n \to \mathbb{R} ^m }$ is surjective.
We see the rank of the derivative

\[{ \text{rk}(Df(x _0)) = m \leq n . }\]

Since the columns of the derivative

\[{ \begin{aligned} Df(x _0) = &\, \begin{pmatrix} D _1 f _1 (x _0) &\cdots &D _n f _1 (x _0) \\ \vdots &\ddots &\vdots \\ D _1 f _m (x _0) &\cdots &D _n f _m (x _0) \end{pmatrix} = [Df(x _0) _1, \ldots, Df(x _0) _n] \end{aligned} }\]

span ${ \mathbb{R} ^m , }$ we can pick indices ${ j _1 < \ldots < j _m }$ such that

\[{ [Df(x _0) _{j _1}, \ldots, Df(x _0) _{j _m}] \, \text{ is a basis of } \mathbb{R} ^m . }\]

Let ${ J }$ be this index set ${ J = \lbrace j _1, \ldots, j _m \rbrace . }$

For a point ${ x = (x _1, \ldots, x _n) }$ in ${ \mathbb{R} ^n }$ and a subset ${ S \subseteq [n], }$ we can write ${ x _S }$ to denote ${ (x _1, \ldots, x _n) }$ after retaining only those ${ x _i }$s with ${ i \in S . }$

By implicit function theorem, there are open neighbourhoods

\[{ x _0 \in \mathscr{U} \subseteq U, \quad (x _0) _{[n] \setminus J} \in \mathscr{V} \subseteq \mathbb{R} ^{n - m} }\]

and a ${ C ^p }$ map

\[{ g : \mathscr{V} \longrightarrow \mathbb{R} ^{m} }\]

such that

\[{ \begin{aligned} &\, Z _f \cap \mathscr{U} \\ = &\, \lbrace (x _1, \ldots, x _{j _1 - 1}, g _1 (x _{[n] \setminus J}), x _{j _1 + 1}, \ldots, x _n) : x _{[n] \setminus J} \in \mathscr{V} \rbrace . \end{aligned} }\]

Formally, we apply implicit function theorem to the function with permuted inputs

\[{ \tilde{f}(x _{[n] \setminus J}; x _J) = f(x _1, \ldots, x _n) . }\]

This function satisfies

\[{ \tilde{f}((x _0) _{[n] \setminus J}; (x _0) _J) = 0 }\]

and that

\[{ \partial _2 \tilde{f} ((x _0) _{[n] \setminus J}; (x _0) _J) = [Df(x _0) _{j _1}, \ldots, Df(x _0) _{j _m}] }\]

is nonsingular. So locally near ${ ((x _0) _{[n] \setminus J}; (x _0) _J ) }$ the zero set ${ Z _{\tilde{f}} }$ looks like the graph of a ${ C ^p }$ map ${ \tilde{\mathscr{V}} (\subseteq \mathbb{R} ^{n-m}) \to \mathbb{R} ^m . }$ Permuting the coordinates in this statement gives that locally near ${ x _0 }$ the zero set ${ Z _f }$ looks as mentioned above.

So informally there are ${ m }$ variables ${ x _{j _1}, \ldots, x _{j _m} }$ that uniquely solve the system of equations

\[{ \begin{aligned} &\, f _1 (x _1, \ldots, x _n) = 0, \\ &\, \quad \quad \vdots \\ &\, f _m (x _1, \ldots, x _n) = 0 \end{aligned} }\]

in a neighbourhood of ${ x _0 }$ as ${ C ^p }$ functions of the other ${ n - m }$ variables.

This suggests the following definition.

Def [Regular points]:
Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a differentiable map.
We say ${ x \in U }$ is a regular point of ${ f }$ if the derivative ${ Df(x) \in L(\mathbb{R} ^n , \mathbb{R} ^m) }$ is surjective. We say ${ f }$ is a submersion if every point in ${ U }$ is regular.
We say ${ y \in \mathbb{R} ^m }$ is a regular value of ${ f }$ if the fiber ${ f ^{ -1} (y) }$ consists entirely of regular points.

Obs: Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^p }$ map. Let ${ x _0 \in Z _f }$ be a regular point of ${ f . }$
Then ${ n \geq m, }$ and there are ${ m }$ variables ${ x _{j _1}, \ldots, x _{j _m} }$ that uniquely solve the system of equations

\[{ \begin{aligned} &\, f _1 (x _1, \ldots, x _n) = 0, \\ &\, \quad \quad \vdots \\ &\, f _m (x _1, \ldots, x _n) = 0 \end{aligned} }\]

in a neighbourhood of ${ x _0 }$ as ${ C ^p }$ functions of the other ${ n - m }$ variables.

Obs: Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^p }$ map. Let ${ 0 \in \text{im}(f) }$ be a regular value of ${ f . }$
Then for every ${ x _0 \in f ^{-1} (0) }$ there is a neighbourhood ${ x _0 \in \mathscr{U} }$ such that ${ f ^{-1} (0) \cap \mathscr{U} }$ is in the above sense the graph of a ${ C ^p }$ function of ${ n - m }$ variables.

Back to top.

\[{ \underline{\textbf{Manifolds}} }\]

Obs [Subspace topology]:
Let ${ (X, d) }$ be a metric space and ${ A \subseteq X . }$ Now ${ (A, d) }$ is a metric space, and we can study its open sets. For ${ a \in A }$ and ${ r > 0 , }$ we have

\[{ \begin{aligned} &\, B _A (a, r) \\ = &\, \lbrace x \in A : d(a, x) < r \rbrace \\ = &\, A \cap B _X (a, r) . \end{aligned} }\]

Hence any open set in ${ (A, d) }$ is of the form ${ A \cap U }$ where ${ U }$ is an open set in ${ (X, d) .}$
Conversely, any set of this form is an open set in ${ (A, d) }$: Let ${ a \in A \cap U }$ where ${ U }$ is open in ${ X . }$ There is an ${ r > 0 }$ such that ${ B _X (a, r) \subseteq U . }$ Hence ${ A \cap B _X (a, r) \subseteq A \cap U }$ that is ${ B _A (a, r) \subseteq A \cap U, }$ as needed.

Def [Submanifolds of ${ \mathbb{R} ^n }$]:
Let ${ M \subseteq \mathbb{R} ^n . }$ We say ${ M }$ is an ${ m }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^n }$ if, for every ${ x _0 \in M ,}$ there are open sets

\[{ x _0 \in U \subseteq \mathbb{R} ^n, \quad V \subseteq \mathbb{R} ^n }\]

and a ${ C ^p }$ isomorphism

\[{ \varphi : U \longrightarrow V }\]

such that

\[{ \varphi (U \cap M) = V \cap (\mathbb{R} ^m \times \lbrace 0 \rbrace) . }\]

Here ${ U \cap M }$ is an open set in ${ M }$ containing ${ x _0, }$ and ${ V \cap (\mathbb{R} ^m \times \lbrace 0 \rbrace) }$ is an open set in ${ \mathbb{R} ^m \times \lbrace 0 \rbrace . }$

We will later show dimension of a non-empty manifold is uniquely determined.

Obs [Open subsets are manifolds]:
Let ${ M \subseteq \mathbb{R} ^n . }$ Then ${ M }$ is an ${ n }$ dimensional ${ C ^{\infty} }$ submanifold of ${ \mathbb{R} ^n }$ if and only if ${ M }$ is an open subset of ${ \mathbb{R} ^n . }$
Pf: ${ \underline{\Rightarrow} }$ Say ${ M }$ is an ${ n }$ dimensional ${ C ^{\infty} }$ submanifold of ${ \mathbb{R} ^n . }$ Let ${ x _0 \in M . }$ There are open sets ${ x _0 \in U }$ and ${ V }$ in ${ \mathbb{R} ^n }$ and a ${ C ^\infty }$ isomorphism ${ \varphi : U \to V }$ such that ${ \varphi(U \cap M) = V . }$ Now ${ U \cap M }$ ${ = \varphi ^{-1} (V) }$ ${ = U }$ that is ${ x _0 \in U \subseteq M , }$ as needed.
${ \underline{\Leftarrow} }$ Say ${ M }$ is an open subset of ${ \mathbb{R} ^n . }$ Let ${ x _0 \in M . }$ Now there are open sets ${ x _0 \in U := M }$ and ${ V := M }$ and a ${ C ^\infty}$ isomorphism ${ \varphi = \text{id} _M : U \to V }$ such that ${ \varphi (U \cap M) = V , }$ as needed.

Obs [Finite subsets are manifolds]:
Let ${ x _1, \ldots, x _k }$ be distinct points in ${ \mathbb{R} ^n . }$ Then ${ M = \lbrace x _1, \ldots, x _k \rbrace }$ is a ${ 0 }$ dimensional ${ C ^{\infty} }$ submanifold of ${ \mathbb{R} ^n . }$
Pf: Let ${ y \in M . }$ Let ${ r }$ ${ = \frac{1}{2} \min \lbrace \lVert x _i - x _j \rVert : i \neq j \rbrace }$ ${ > 0 . }$
Now there are open sets ${ y \in U := B(y, r) }$ and ${ V := B(0, r) }$ and a ${ C ^{\infty} }$ isomorphism ${ \varphi : U \to V, }$ ${ \varphi (x) = x - y }$ such that ${ \varphi (U \cap M) }$ ${ = \varphi (\lbrace y \rbrace ) }$ ${ = \lbrace 0 \rbrace , }$ as needed.

Obs: Let ${ \psi : \mathbb{R} ^n \to \mathbb{R} ^n }$ be a ${ C ^p }$ isomorphism and ${ M }$ an ${ m }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^n . }$
Then ${ \psi(M) }$ is an ${ m }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^n . }$
Pf: Let ${ \psi(x _0) \in \psi(M) . }$ There are open sets ${ x _0 \in U }$ and ${ V }$ and a ${ C ^p }$ isomorphism ${ \varphi : U \to V }$ such that the patch ${ \varphi(U \cap M) = V \cap (\mathbb{R} ^m \times \lbrace 0 \rbrace). }$ So there are open sets

\[{ \psi (x _0) \in \psi(U) \subseteq \mathbb{R} ^n , \quad V \subseteq \mathbb{R} ^n }\]

and a ${ C ^p }$ isomorphism

\[{ \tilde{\varphi} : \psi(U) \longrightarrow V, \quad \tilde{\varphi} = \varphi \circ \psi ^{-1} }\]

such that the patch

\[{ \begin{aligned} &\, \tilde{\varphi} (\psi(U) \cap \psi(M)) \\ = &\, \varphi(U \cap M) \\ = &\, V \cap (\mathbb{R} ^m \times \lbrace 0 \rbrace ) , \end{aligned} }\]

as needed. ${ \blacksquare }$

Thm [Graphs are manifolds]:
Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^p }$ map. Then ${ \text{graph} (f) }$ is an ${ n }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^{n+m} . }$
Pf: Consider the open set ${ \mathscr{U} = U \times \mathbb{R} ^m . }$ It suffices to find a ${ C ^p }$ isomorphism

\[{ \text{Want:} \quad \begin{aligned} &\, \text{A } C ^p \text{ isomorphism } \varphi : \mathscr{U} \longrightarrow \mathscr{U} \\ &\, \text{with } \varphi(\mathscr{U} \cap \text{graph}(f)) = \mathscr{U} \cap (\mathbb{R} ^n \times \lbrace 0 \rbrace ) . \end{aligned} }\]

Informally, we want a ${ C ^p }$ isomorphism ${ \varphi : \mathscr{U} \longrightarrow \mathscr{U} }$ which sends points ${ (x, f(x)) }$ in ${ \mathscr{U} \cap \text{graph}(f) }$ to points for which last ${ m }$ coordinates are ${ 0 . }$

So we can naturally consider

\[{ \varphi : \mathscr{U} \longrightarrow \mathbb{R} ^{n + m}, \quad \varphi(x, y) = (x, y - f(x)) . }\]

The image of the map is ${ \text{im}(\varphi) = \mathscr{U} . }$ Also for ${ (\mathbf{x}, \mathbf{y}) \in \mathscr{U}, }$ the fiber

\[{ \begin{aligned} &\, \varphi ^{-1} ((\mathbf{x}, \mathbf{y})) \\ = &\, \lbrace (x, y) \in \mathscr{U} : (x, y - f(x)) = (\mathbf{x}, \mathbf{y}) \rbrace \\ = &\, \lbrace (\mathbf{x}, f(\mathbf{x}) + \mathbf{y}) \rbrace . \end{aligned} }\]

Hence ${ \varphi : \mathscr{U} \longrightarrow \mathscr{U} }$ is a ${ C ^p }$ bijection with a ${ C ^p }$ inverse, that is

\[{ \varphi : \mathscr{U} \longrightarrow \mathscr{U} \, \, \text{ is a } C ^p \text{ isomorphism.} }\]

Further, the patch

\[{ \begin{aligned} &\, \varphi(\mathscr{U} \cap \text{graph}(f)) \\ = &\, \lbrace \varphi(x, f(x)) : x \in U \rbrace \\ = &\, \lbrace (x, 0) : x \in U \rbrace \\ = &\, \mathscr{U} \cap (\mathbb{R} ^n \times \lbrace 0 \rbrace ) \end{aligned} }\]

as needed. ${ \blacksquare }$

Obs [Regular fibers are manifolds]:
Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^p }$ map. Let ${ c \in \text{im}(f) }$ be a regular value of ${ f . }$
Then ${ f ^{-1} (c) }$ is an ${ n-m }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^n . }$
Pf: Recall ${ f ^{-1} (c) }$ is locally the graph of a ${ C ^p }$ function of ${ n - m }$ variables, and that graphs are manifolds. So we are done.

Eg: The spheres ${ S ^{n-1} }$ are regular fibers, and therefore are manifolds.

Eg [The orthogonal groups are manifolds]:
The orthogonal group

\[{ O _n = \lbrace A \in \mathbb{R} ^{n \times n} : A ^T A = I _n \rbrace }\]

is a ${ C ^{\infty} }$ submanifold of ${ \mathbb{R} ^{n \times n} }$ of dimension ${ n(n-1)/2 . }$
Pf: We see the orthogonal group ${ O _n }$ is the fiber ${ f ^{-1} (I _n) }$ for the map

\[{ f : \mathbb{R} ^{n \times n} \longrightarrow \mathbb{R} ^{n \times n} _{\text{sym}}, \quad f(A) = A ^T A . }\]

The space of symmetric matrices ${ \mathbb{R} _{\text{sym}} ^{n \times n} }$ has dimension equal to the number of upper triangular positions (in an ${ n \times n }$ matrix), namely ${ 1 + \ldots + n }$ ${ = \frac{n(n+1)}{2} . }$
Note that ${ f }$ is smooth, because ${ f (A) = g(A, A) }$ where ${ g }$ is the continuous bilinear map

\[{ g : \mathbb{R} ^{n \times n} \times \mathbb{R} ^{n \times n} \longrightarrow \mathbb{R} ^{n \times n}, \quad g(A, B) = A ^T B . }\]

Considering the composition

\[{ A \overset{\alpha}{\longmapsto} (A, A) \overset{g}{\longmapsto} A ^T A }\]

the derivative of ${ f }$ is given by

\[{ \begin{aligned} &\, Df(A) \, H \\ = &\, Dg(\alpha(A)) \circ D\alpha (A) \, H \\ = &\, Dg (\alpha(A)) \, (H, H) \\ = &\, H ^T A + A ^T H \end{aligned} }\]

for ${ A, H \in \mathbb{R} ^{n \times n} . }$
Now note that ${ I _n }$ is a regular value of ${ f . }$

Let ${ A \in f ^{-1} (I _n) . }$ We are to show

\[{ \text{To show: } \quad Df(A) : \mathbb{R} ^{n \times n} \longrightarrow \mathbb{R} ^{n \times n} _{\text{sym}} \, \, \text{ is surjective}. }\]

Let ${ S \in \mathbb{R} ^{n \times n} _{\text{sym}} . }$ For ${ H = AS/2 }$ we have

\[{ \begin{aligned} &\, Df(A) \, H \\ = &\, H ^T A + A ^T H \\ = &\, \frac{1}{2} S ^T A ^T A + \frac{1}{2} A ^T A S \\ = &\, S , \end{aligned} }\]

as needed.

Hence the regular fiber ${ O _n = f ^{-1} (I _n) }$ is an ${ n ^2 - \frac{n(n+1)}{2} }$ dimensional ${ C ^{\infty} }$ submanifold of ${ \mathbb{R} ^{n \times n} . }$

Def [Immersions]:
Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^1 }$ map.
We say ${ f }$ is an immersion if ${ Df(x) \in L(\mathbb{R} ^n, \mathbb{R} ^m) }$ is injective for all ${ x \in U . }$

Thm [Immersions produce manifolds]:
Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^p }$ immersion.
Then for every ${ x _0 \in U }$ there is an open neighbourhood ${ x _0 \in \mathscr{U} \subseteq U }$ such that ${ f(\mathscr{U}) }$ is an ${ n }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^m . }$

Pf: Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^p }$ immersion. Let ${ x _0 \in U . }$ Now note the derivative

\[{ Df(x _0) = \begin{pmatrix} D _1 f _1 (x _0) &\cdots &D _n f _1 (x _0) \\ \vdots &\ddots &\vdots \\ D _1 f _m (x _0) &\cdots &D _n f _m (x _0) \end{pmatrix} }\]

has rank

\[{ \text{rk}(Df(x _0)) = n \leq m . }\]

Since the rows of ${ Df(x _0) }$ span ${ \mathbb{R} ^n , }$ we can pick indices ${ i _1 < \ldots < i _n }$ such that

\[{ \text{The rows } Df(x _0) _{i _1, \ast}, \ldots, Df(x _0) _{i _n, \ast} \, \text{ form a basis of } \mathbb{R} ^n . }\]

Let ${ I }$ be this index set ${ I = \lbrace i _1, \ldots, i _n \rbrace . }$

For the function with permuted outputs

\[{ \tilde{f} : U (\subseteq \mathbb{R} ^n \text{ open}) \longrightarrow \mathbb{R} ^m, }\] \[{ \tilde{f}(x) = (f(x) _I; f(x) _{[m] \setminus I}) }\]

the top ${ n }$ by ${ n }$ block of ${ D \tilde{f} (x _0) }$ is nonsingular.

In an attempt to “complete” the map

\[{ \tilde{f} : U (\subseteq \mathbb{R} ^n \text{ open}) \longrightarrow \mathbb{R} ^m }\]

to a map

\[{ U \times \mathbb{R} ^{m - n} (\subseteq \mathbb{R} ^m \text{ open}) \longrightarrow \mathbb{R} ^m }\]

which is locally invertible at ${ (x _0, 0) }$ i.e. has nonsingular derivative at ${ (x _0, 0) , }$ we can consider

\[{ \psi : U \times \mathbb{R} ^{m-n} (\subseteq \mathbb{R} ^m \text{ open}) \longrightarrow \mathbb{R} ^m, }\] \[{ \psi(x, y) = \tilde{f}(x) + (0, y) }\]

that is

\[{ \psi(x, y) = (\tilde{f} _1 (x), \ldots, \tilde{f} _n (x); \tilde{f} _{n+1} (x) + y _1, \ldots, \tilde{f} _m (x) + y _{m-n}) . }\]

The derivative of this map at ${ (x _0, 0) }$ looks like

\[{ D\psi (x _0, 0) = \begin{pmatrix} A &0 \\ B &I _{m - n} \end{pmatrix} }\]

where

\[{ A = \begin{pmatrix} D _1 \tilde{f} _1 (x _0) &\cdots &D _n \tilde{f} _1 (x _0) \\ \vdots &\ddots &\vdots \\ D _1 \tilde{f} _n (x _0) &\cdots &D _n \tilde{f} _n (x _0) \end{pmatrix} \, \text{ is nonsingular} }\]

and

\[{ B = \begin{pmatrix} D _1 \tilde{f} _{n+1} (x _0) &\cdots &D _n \tilde{f} _{n+1} (x _0) \\ \vdots &\ddots &\vdots \\ D _1 \tilde{f} _m (x _0) &\cdots &D _n \tilde{f} _m (x _0) \end{pmatrix} . }\]

Therefore ${ D\psi (x _0, 0) }$ is nonsingular, as needed.

By inverse function theorem, ${ \psi : U \times \mathbb{R} ^{m - n} (\subseteq \mathbb{R} ^m \text{ open}) \longrightarrow \mathbb{R} ^m }$ is a local ${ C ^p }$ isomorphism at ${ (x _0, 0) . }$ There exist open neighbourhoods

\[{ (x _0, 0) \in W \subseteq U \times \mathbb{R} ^{m - n}, \quad \tilde{f}(x _0) \in W ^{’} \subseteq \mathbb{R} ^m }\]

such that ${ \psi \big\vert _W : W \longrightarrow W ^{’} }$ is a ${ C ^p }$ isomorphism.

Let ${ \varphi = (\psi \big\vert _{W ^{’}} ) ^{-1} : W ^{’} \longrightarrow W . }$ Now we have

\[{ W _0 := \lbrace x \in \mathbb{R} ^n : (x, 0) \in W \rbrace }\]

is an open neighbourhood of ${ x _0 , }$ with image

\[{ \begin{aligned} &\, \tilde{f}(W _0) \\ = &\, \lbrace \tilde{f}(x) : (x, 0) \in W \rbrace \\ = &\, \lbrace \psi(x, 0) : (x, 0) \in W \rbrace \\ = &\, \psi (W _0 \times \lbrace 0 \rbrace ). \end{aligned} }\]

Further

\[{ \begin{aligned} &\, \varphi (W ^{’} \cap \tilde{f}(W _0)) \\ = &\, \varphi (W ^{’} \cap \psi (W _0 \times \lbrace 0 \rbrace )) \\ = &\, \varphi(\psi(W _0 \times \lbrace 0 \rbrace)) \\ = &\, W _0 \times \lbrace 0 \rbrace \\ = &\, W \cap (\mathbb{R} ^n \times \lbrace 0 \rbrace ) . \end{aligned} }\]

Hence ${ \tilde{f}(W _0) }$ is an ${ n }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^m . }$
Permuting coordinates gives that ${ f(W _0) }$ is an ${ n }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^m , }$ as needed. ${ \blacksquare }$

Review: Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^ p }$ immersion. Let ${ x _0 \in U . }$

By the nature of ${ Df(x _0) }$ we can pick indices ${ I = \lbrace i _1 < \ldots < i _n \rbrace }$ such that rows ${ i _1, \ldots, i _n }$ of ${ Df(x _0) }$ form a nonsingular matrix. Now letting

\[{ \tilde{f}(x) := (f(x) _I; f(x) _{[m] \setminus I}) }\]

note that

\[{ \psi : U \times \mathbb{R} ^{m - n} \longrightarrow \mathbb{R} ^m, \quad \psi(x, y) := \tilde{f}(x) + (0, y) }\]

is a local ${ C ^p }$ isomorphism at ${ (x _0, 0) . }$ So there are open sets

\[{ (x _0, 0) \in W \subseteq U \times \mathbb{R} ^{m - n}, \quad \tilde{f}(x _0) \in W ^{’} \subseteq \mathbb{R} ^m }\]

such that ${ \psi \big\vert _{W} : W \longrightarrow W ^{’} }$ is a ${ C ^p }$ isomorphism.

To summarise, there are open sets ${ (x _0, 0) \in W }$ and ${ W ^{’} }$ in ${ \mathbb{R} ^m }$ and a ${ C ^p }$ isomorphism ${ W \longrightarrow W ^{’} }$ such that

\[{ \psi (x, 0) = \tilde{f}(x) \quad \text{ for } (x, 0) \in W . }\]

Permuting output coordinates of ${ \psi }$ appropriately, there are open sets ${ (x _0, 0) \in W }$ and ${ \tilde{W ^{’} }}$ in ${ \mathbb{R} ^m }$ and a ${ C ^p }$ isomorphism ${ W \longrightarrow \tilde{W ^{’}} }$ such that

\[{ \tilde{\psi}(x, 0) = f(x) \quad \text{ for } (x, 0) \in W . }\]

This is the main observation, that “near ${ (x _0, 0 ) }$ we can extend the immersion ${ \mathbb{R} ^n \to \mathbb{R} ^m }$ to a ${ C ^p }$ isomorphism ${ \mathbb{R} ^m \to \mathbb{R} ^m }$”.

Now considering ${ W _0 = \lbrace x \in \mathbb{R} ^n : (x, 0) \in W \rbrace }$ and the image

\[{ f(W _0) = \tilde{\psi}(W _0 \times \lbrace 0 \rbrace ) }\]

and the ${ C ^p }$ isomorphism ${ \tilde{\psi} ,}$ we get that ${ f(W _0) }$ is an ${ n }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^m . }$

Def [Embeddings]:
Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^1 }$ map.
We say ${ f }$ is an embedding if it is an immersion and ${ f : U \to f(U) }$ is a homeomorphism.

Eg [Injective immersions need not be embeddings]:
Consider the curve

\[{ f : \left( - \frac{\pi}{4}, \frac{\pi}{2} \right) \longrightarrow \mathbb{R} ^2, \, \, f(t) = \sin 2t \, (-\sin t, \cos t ) . }\]

Here is a gif for the curve made using python and imagemagick, as in this tutorial.

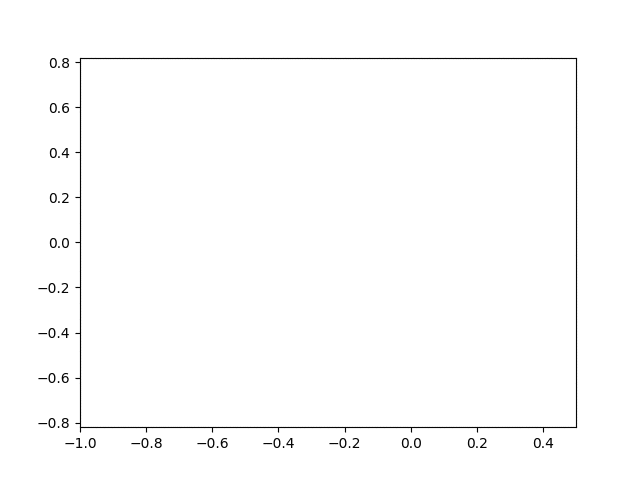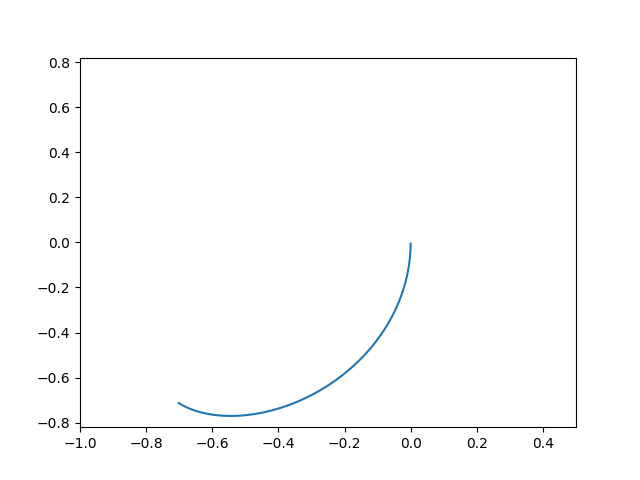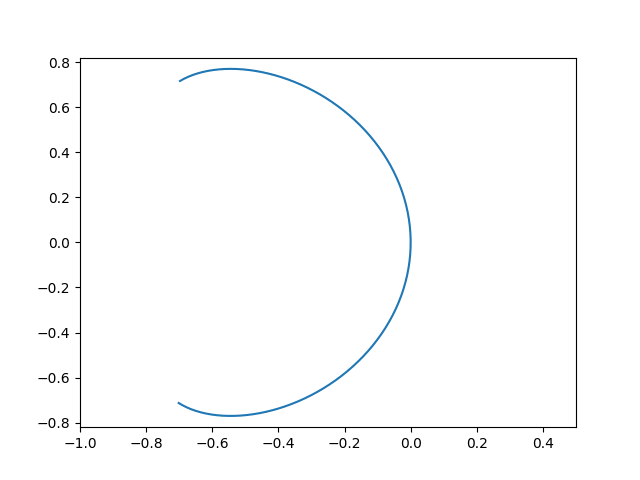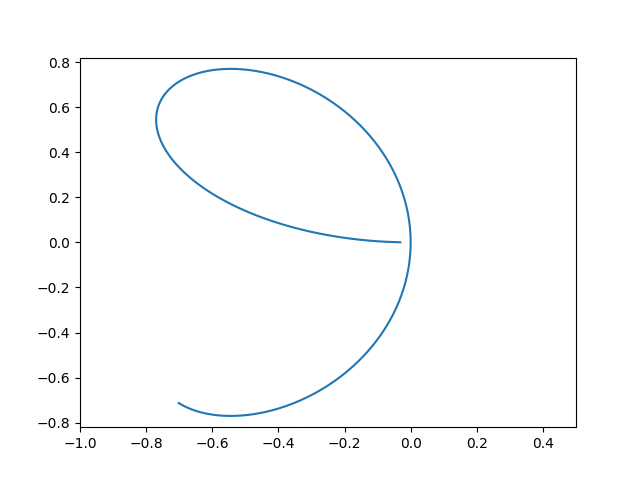
The python code is given below.

import mathplotlib.pyplot as plt 
import math
N = 300 
x = list(range(N)) 
y = list(range(N)) 
a = - (math.pi) / 4 
b = (math.pi) / 2 
for i in range(N):
    x[i] = math.sin(2 * (a + (b-a)/(N+1) * (i+1))) * (-math.sin(a + (b-a)/(N+1) * (i+1)))
    y[i] = math.sin(2 * (a + (b-a)/(N+1) * (i+1))) * math.cos(a + (b-a)/(N+1) * (i+1))
!mkdir images 
for i in range(N): 
    ax = plt.plot(x[:i], y[:i]) 
    plt.xlim((-1, 0.5))
    plt.ylim((min(y) - 0.05, max(y) + 0.05))
    plt.savefig(f`images/{i:003}’, dpi = 100) 
!magick -delay 5 images/*.png immersion.gif

Note that ${ f }$ is an injective ${ C ^{\infty} }$ immersion, but the inverse ${ f ^{-1} : f(U) \to U }$ isn’t continuous at ${ (0, 0) . }$

\[{ }\]

Thm [Image of an embedding is a manifold]:
Let ${ f : U (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^m }$ be a ${ C ^p }$ embedding.
Then ${ f(U) }$ is an ${ n }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^m . }$
Pf: Let ${ y _0 \in f(U) . }$
By the previous result, ${ x _0 := f ^{-1} (y _0) }$ has an open neighbourhood ${ x _0 \in U _0 \subseteq U }$ such that ${ f(U _0) }$ is an ${ n }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^m . }$
By definition there are open sets ${ y _0 \in U _1 }$ and ${ V _1 }$ and a ${ C ^p }$ isomorphism ${ \varphi : U _1 \to V _1 }$ such that the patch ${ \varphi (U _1 \cap f(U _0)) = V _1 \cap (\mathbb{R} ^n \times \lbrace 0 \rbrace) .}$
Since ${ f : U \to f(U) }$ is a homeomorphism, ${ f(U _0) }$ is an open set wrt ${ f(U) . }$ There is an open set ${ U _2 }$ such that ${ f(U _0) = f(U) \cap U _2 . }$
Now note the above equation can be rewritten as ${ \varphi (U _1 \cap U _2 \cap f(U)) = \varphi(U _1) \cap (\mathbb{R} ^n \times \lbrace 0 \rbrace ) . }$
Hence there are open sets ${ y _0 \in \mathscr{U} := U _1 \cap U _2 }$ and ${ \mathscr{V} := \varphi(U _1 \cap U _2) }$ and a ${ C ^p }$ isomorphism ${ \Phi = \varphi \big\vert _{\mathscr{U}} : \mathscr{U} \to \mathscr{V} }$ such that the patch

\[{ \begin{aligned} &\, \Phi (\mathscr{U} \cap f(U)) \quad (\subseteq \mathscr{V}) \\ = &\, \varphi(U _1) \cap (\mathbb{R} ^{n} \times \lbrace 0 \rbrace ) \\ = &\, \mathscr{V} \cap (\mathbb{R} ^n \times \lbrace 0 \rbrace ) , \end{aligned} }\]

as needed. ${ \blacksquare }$

Obs [Every manifold is locally the image of an embedding]:
Let ${ M }$ be an ${ m }$ dimensional ${ C ^p }$ submanifold of ${ \mathbb{R} ^n . }$ Let ${ x _0 \in M . }$ Then there is an open set ${ x _0 \in U }$ wrt ${ M }$ which is the image of an open set in ${ \mathbb{R} ^m }$ under a ${ C ^p }$ embedding.
Pf: There are open sets ${ x _0 \in \tilde{U} }$ and ${ \tilde{V} }$ in ${ \mathbb{R} ^n }$ and a ${ C ^p }$ isomorphism ${ \varphi : \tilde{U} \to \tilde{V} }$ such that the patch ${ \varphi (\tilde{U} \cap M ) = \tilde{V} \cap (\mathbb{R} ^m \times \lbrace 0 \rbrace ) . }$
Now note that ${ x _0 \in U := \tilde{U} \cap M }$ and ${ V := \lbrace x \in \mathbb{R} ^m : (x, 0) \in \tilde{V} \rbrace }$ are open sets wrt ${ M }$ and ${ \mathbb{R} ^m }$ respectively, and

\[{ g : V (\subseteq \mathbb{R} ^m \text{ open}) \longrightarrow \mathbb{R} ^n , }\] \[{ g(x) := \varphi ^{-1} ((x, 0)) }\]

is a ${ C ^p }$ embedding with image ${ g(V) = U .}$
For example, to show ${ g }$ is an immersion: For every ${ x \in V }$ the derivative

\[{ D g (x) : \mathbb{R} ^m \longrightarrow \mathbb{R} ^n }\]

is given by

\[{ Dg(x) = D(\varphi ^{-1}) \, (x, 0) \circ (t \mapsto (t, 0)) }\]

that is

\[{ Dg(x) \, h = (\text{first } m \text{ columns of } D(\varphi ^{-1}) (x, 0)) \, h . }\]

Hence ${ Dg(x) }$ is injective for all ${ x \in V , }$ as needed. ${ \blacksquare }$

We saw image of an embedding is a manifold, and every manifold is locally the image of an embedding. Hence embeddings (i.e. “immersions which preserve topological structure”) are fundamental to the study of manifolds.

This suggests the following definition.

Def [Local charts]:
Let ${ M \subseteq \mathbb{R} ^n }$ and ${ p \in M .}$ We denote by ${ i _M }$ the inclusion map

\[{ i _M : M \longrightarrow \mathbb{R} ^n, \quad x \mapsto x . }\]

A map ${ \varphi }$ is called an ${ m }$ dimensional local ${ C ^q }$ chart of ${ M }$ near ${ p }$ if:

• ${ U := \text{dom}(\varphi) }$ is an open neighbourhood of ${ p }$ wrt ${ M . }$
• ${ \varphi }$ is a homeomorphism of ${ U }$ onto an open set ${ V := \varphi(U) }$ of ${ \mathbb{R} ^m . }$
• ${ g := i _M \circ \varphi ^{-1} }$ is a ${ C ^q }$ immersion.

Here is an equivalent definition. Let ${ M \subseteq \mathbb{R} ^n }$ and ${ p \in M . }$
A bijection ${ \varphi : U \to V }$ such that ${ p \in U }$ is called an ${ m }$ dimensional local ${ C ^q }$ chart of ${ M }$ near ${ p }$ if:

• ${ U }$ and ${ V }$ are open sets wrt ${ M }$ and ${ \mathbb{R} ^m }$ respectively.
• ${ g := i _M \circ \varphi ^{-1} }$ is a ${ C ^q }$ embedding.

The set ${ U }$ is the charted territory of ${ \varphi , }$ ${ \, V }$ is the parameter range, and ${ g }$ is the parameterisation of ${ U }$ in ${ \varphi . }$ Further ${ (x _1, \ldots, x _m) := \varphi(p) }$ are called the local coordinates of ${ p \in U }$ in the chart ${ \varphi . }$

Def [Atlas]:
Let ${ M \subseteq \mathbb{R} ^n .}$ An ${ m }$ dimensional ${ C ^q }$ atlas for ${ M }$ is a collection ${ \lbrace \varphi _{\alpha} : \alpha \in \mathsf{A} \rbrace }$ of ${ m }$ dimensional ${ C ^q }$ charts of ${ M , }$ whose charted territories ${ U _{\alpha} := \text{dom}(\varphi _{\alpha}) }$ cover the set ${ M }$ that is ${ M = \cup _{\alpha} U _{\alpha} .}$

Obs [Every manifold has an atlas]:
Let ${ M }$ be an ${ m }$ dimensional ${ C ^q }$ submanifold of ${ \mathbb{R} ^n . }$ By the previous result, for every ${ p \in M }$ there is an ${ m }$ dimensional ${ C ^q }$ chart of ${ M }$ near ${ p . }$ Therefore ${ M }$ has an ${ m }$ dimensional ${ C ^q }$ atlas.

Def [Transition functions]:
Let ${ \lbrace (\varphi _{\alpha}, U _{\alpha}) : \alpha \in \mathsf{A} \rbrace }$ be an ${ m }$ dimensional ${ C ^q }$ atlas for ${ M \subseteq \mathbb{R} ^n . }$ We call the maps

\[{ \varphi _{\beta} \circ \varphi _{\alpha} ^{-1} : \varphi _{\alpha} (U _{\alpha} \cap U _{\beta}) \longrightarrow \varphi _{\beta} (U _{\alpha} \cap U _{\beta}) \quad \text{ for } \alpha, \beta \in \mathsf{A} }\]

transition functions. Informally, they describe how local coordinates change from one chart to another.

Through a chart ${ (\varphi _1, U _1) , }$ the charted territory ${ U _1 }$ can be described using its local coordinates ${ (x _1, \ldots, x _m) = \varphi _1 (p) \in \mathbb{R} ^m }$ for ${ p \in U _1 . }$

If ${ (\varphi _2, U _2) }$ is a second chart, through it ${ U _2 }$ has its own local coordinates ${ (y _1, \ldots, y _m) = \varphi _2 (p) \in \mathbb{R} ^m . }$

Now ${ U _1 \cap U _2 }$ has a description in two coordinate systems ${ (x _1, \ldots, x _m) }$ and ${ (y _1, \ldots, y _m) . }$ The transition function ${ \varphi _2 \circ \varphi _1 ^{-1} }$ is just the coordinate transformation ${ (x _1, \ldots, x _m) \mapsto (y _1, \ldots, y _m) ,}$ that is it converts coordinates in one chart into coordinates in the other chart.

Thm [Transition functions are ${ C ^q }$ isomorphisms]:
Let ${ (\varphi _{\alpha}, U _{\alpha}) }$ and ${ (\varphi _{\beta}, U _{\beta}) }$ be ${ m }$ dimensional ${ C ^q }$ charts of an ${ m }$ dimensional ${ C ^q }$ manifold.
Then the transition function

\[{ \varphi _{\beta} \circ \varphi _{\alpha} ^{-1} : \varphi _{\alpha} (U _{\alpha} \cap U _{\beta}) \longrightarrow \varphi _{\beta} (U _{\alpha} \cap U _{\beta}) }\]

is a ${ C ^q }$ isomorphism. Further, its inverse is ${ (\varphi _{\beta} \circ \varphi _{\alpha} ^{-1} ) ^{-1} = \varphi _{\alpha} \circ \varphi _{\beta} ^{-1} .}$

Pf: It is clear that the set maps ${ \varphi _{\beta} \circ \varphi _{\alpha} ^{-1} }$ and ${ \varphi _{\alpha} \circ \varphi _{\beta} ^{-1} }$ are bijective and are inverses of each other. It is left to show for example that

\[{ \varphi _{\beta} \circ \varphi _{\alpha} ^{-1} : \varphi _{\alpha} (U _{\alpha} \cap U _{\beta}) \longrightarrow \mathbb{R} ^m }\]

is a ${ C ^q }$ map.
Let ${ V _{\gamma} := \varphi _{\gamma} (U _{\gamma}) }$ and ${ g _{\gamma} }$ be the parameterisation belonging to ${ (\varphi _{\gamma}, U _{\gamma}) }$ for ${ \gamma \in \lbrace \alpha, \beta \rbrace . }$
Let ${ p \in U _{\alpha} \cap U _{\beta} .}$ There exist ${ x _{\gamma} \in \varphi _{\gamma} (U _{\alpha} \cap U _{\beta}) }$ such that ${ g _{\alpha} (x _{\alpha}) }$ ${ = g _{\beta} (x _{\beta}) }$ ${ = p . }$
Since ${ g _{\gamma} }$ is a ${ C ^q }$ immersion, there are open sets ${ p \in \tilde{U} _{\gamma} }$ and ${ (x _{\gamma}, 0) \in \tilde{V} _{\gamma} }$ in ${ \mathbb{R} ^n }$ and a ${ C ^q }$ isomorphism ${ \psi _{\gamma} : \tilde{V} _{\gamma} \longrightarrow \tilde{U} _{\gamma} }$ such that

\[{ \psi _{\gamma} (x, 0) = g _{\gamma} (x) \quad \text{ for } (x, 0) \in \tilde{V} _{\gamma} .}\]

We can now “ignore the immersions ${ g _{\gamma} }$ and work with the ${ C ^q }$ isomorphisms ${ \psi _{\gamma} }$”.
We can pick an open neighbourhood ${ x _{\alpha} \in V }$ in ${ \mathbb{R} ^m }$ such that

\[{ x \in V \implies x \in V _{\alpha}, \, \, (x, 0) \in \tilde{V} _{\alpha} }\] \[{ x \in V \implies g _{\alpha} (x) \in U _{\alpha} \cap U _{\beta}, \, \, g _{\alpha} (x) \in \tilde{U} _{\alpha} \cap \tilde{U} _{\beta} . }\]

So for ${ x \in V , }$ the expressions ${ g _{\alpha} (x), }$ ${ \varphi _{\beta} (g _{\alpha} (x)) }$ and ${ \psi _{\alpha} (x, 0) , }$ ${ \psi _{\beta} ^{-1} ( \psi _{\alpha} (x, 0)) }$ all exist. Now

\[{ \begin{aligned} &\, (\varphi _{\beta} \circ \varphi _{\alpha} ^{-1}) \, (x) \\ = &\, \varphi _{\beta} (g _{\alpha} (x)) \\ = &\, (\pi \circ \psi _{\beta} ^{-1} ) \circ (\psi _{\alpha} \circ i) \, (x) \end{aligned} }\]

for ${ x \in V , }$ where

\[{ i : \mathbb{R} ^m \longrightarrow \mathbb{R} ^n, \quad x \mapsto (x, 0) , }\] \[{ \pi : \mathbb{R} ^n \longrightarrow \mathbb{R} ^m, \quad x \mapsto (x _1, \ldots, x _m) . }\]

Hence ${ \varphi _{\beta} \circ \varphi _{\alpha} ^{-1} }$ is a ${ C ^p }$ map over the open neighbourhood ${ x _{\alpha} \in V , }$ as needed. ${ \blacksquare }$

Obs [Dimension of a manifold is uniquely determined]:
Let ${ M }$ be an ${ m }$ dimensional ${ C ^q }$ submanifold of ${ \mathbb{R} ^n }$ and ${ p \in M . }$ There is an ${ m }$ dimensional ${ C ^q }$ chart ${ (\varphi, U) }$ near ${ p . }$ Let ${ (\psi, V) }$ be an ${ m ^{’} }$ dimensional ${ C ^q }$ chart near ${ p . }$ Repeating the above proof shows that the transition function

\[{ \psi \circ \varphi ^{-1} : \underbrace{\varphi(U \cap V)} _{\text{open in } \mathbb{R} ^m} \longrightarrow \underbrace{\psi(U \cap V)} _{\text{open in } \mathbb{R} ^{m ^{’}} } }\]

is a ${ C ^q }$ isomorphism. Now the derivative of the isomorphism at any point is nonsingular, so especially ${ m = m ^{’} }$ as needed. ${ \blacksquare }$

Back to top.

\[{ \underline{\textbf{Tangents and Normals}} }\]

Def [Tangential space of an open subset]:
Let ${ X \subseteq \mathbb{R} ^n }$ be an open subset and ${ p \in X . }$ The tangential space ${ T _p X }$ of ${ X }$ at the point ${ p }$ is the set ${ \lbrace p \rbrace \times \mathbb{R} ^n }$ with the induced Euclidean space structure

\[{ (p, v) + \lambda (p, w) := (p, v + \lambda w) , }\] \[{ ((p, v) \, \vert \, (p, w)) _p := (v \, \vert \, w) }\]

for all ${ (p, v), (p, w) }$ ${ \in T _p X }$ and ${ \lambda \in \mathbb{R} . }$
An element ${ (p, v) \in T _p X }$ is called a tangential vector of ${ X }$ at ${ p }$ and is also written as ${ (v) _p . }$

Def [Tangential of a map]:
Let ${ p \in X \subseteq \mathbb{R} ^n , }$ ${ Y \subseteq \mathbb{R} ^{\ell} }$ be open subsets and ${ f : X \to Y }$ a ${ C ^1 }$ map. Then the linear map

\[{ T _p f : T _p X \longrightarrow T _{f(p)} Y , }\] \[{ (p, v) \mapsto (f(p), Df(p) \, v) }\]

is called the tangential of ${ f }$ at the point ${ p . }$

Obs [Chain rule for Tangentials]:
Let

\[{ X (\subseteq \mathbb{R} ^n \text{ open}) \overset{f}{\longrightarrow} Y (\subseteq \mathbb{R} ^{\ell} \text{ open}) \overset{g}{\longrightarrow} Z (\subseteq \mathbb{R} ^s \text{ open}) }\]

be ${ C ^1 }$ maps and ${ p \in X . }$ By chain rule

\[{ T _p (g \circ f ) = T _{f(p)} g \circ T _p f }\]

that is tangential of composition is composition of tangentials.

Obs [Tangential of an isomorphism]:
Let ${ p \in X \subseteq \mathbb{R} ^n , }$ ${ Y \subseteq \mathbb{R} ^{\ell} }$ be open subsets and ${ f : X \to Y }$ a ${ C ^1 }$ isomorphism.
By chain rule, ${ T _p f : T _p X \to T _{f(p)} Y }$ is a toplinear isomorphism with ${ ( T _p f) ^{-1} = T _{f(p)} f ^{-1} . }$

Def [Tangential space of a manifold]:
Let ${ M }$ be an ${ m }$ dimensional ${ C ^q }$ submanifold of ${ \mathbb{R} ^n , }$ and ${ p \in M , }$ and ${ (\varphi, U) }$ is a chart near ${ p ,}$ and ${ (g, V) }$ is the parameterisation belonging to ${ (\varphi, U) . }$
Now the tangential space ${ T _p M }$ of ${ M }$ at the point ${ p }$ is the image of the tangential space ${ T _{\varphi(p)} V }$ under the tangential ${ T _{\varphi(p)} g , }$ that is

\[{ T _p M = \text{im}(T _{\varphi(p)} g) . }\]

We will later show that ${ T _p M }$ is well defined and independent of the chosen chart ${ (\varphi, U) . }$
Here elements of ${ T _p M }$ are called tangential vectors of ${ M }$ at ${ p , }$ and union of all the tangential spaces

\[{ T M = \bigcup _{p \in M} T _p M }\]

is called the tangent bundle of ${ M . }$

Obs [${ T_p M }$ is independent of the chosen chart ${ \varphi }$]:
In the context of the above definition, say ${ (\tilde{\varphi}, \tilde{U}) }$ is another chart of ${ M }$ near ${ p }$ with associated parameterisation ${ (\tilde{g}, \tilde{V}) . }$ WLOG ${ U }$ and ${ \tilde{U} }$ coincide, because otherwise we can consider ${ U \cap \tilde{U} }$ and restrictions of charts on this.
We are to show the tangential images

\[{ \text{To show: } \quad \text{im}(T _{\varphi(p)} g) = \text{im}(T _{\tilde{\varphi}(p)} \tilde{g}) . }\]

By definition of a tangential, any ${ C ^1 }$ map ${ f : X \to Y }$ between open sets and a point ${ p \in X }$ induces a tangential map ${ T _p f : T _p X \to T _{f(p)} Y }$ sending ${ (p, v) \mapsto (f(p), Df(p) \, v) . }$
So by chain rule, the commutative diagram of mappings

induces the commutative diagram of tangentials

Here the transition function

\[{ \tilde{\varphi} \circ \varphi ^{-1} : V \longrightarrow \tilde{V} }\]

is a ${ C ^q }$ isomorphism, hence the tangential ${ T _{\varphi(p)} (\tilde{\varphi} \circ \varphi ^{-1}) }$ is a linear isomorphism. Hence the linear maps ${ T _{\varphi(p)} g }$ and ${ T _{\tilde{\varphi}(p)} \tilde{g} }$ have the same images, as needed. ${ \blacksquare }$

Obs: If ${ M }$ is an open subset of ${ \mathbb{R} ^n }$ and ${ p \in M, }$ the above definitions of tangential space of an open subset and tangential space of a manifold agree.

Obs [Tangential of a chart]:
Let ${ M }$ be an ${ m }$ dimensional ${ C ^q }$ submanifold of ${ \mathbb{R} ^n , }$ and ${ p \in M , }$ and ${ (\varphi, U) }$ is a chart of ${ M }$ near ${ p }$ with associated parameterisation ${ (g, V) . }$
Note ${ T _{\varphi (p)} g : T _{\varphi (p)} V \to T _{p} \mathbb{R} ^n }$ is injective with image ${ T _p M = \text{im}(T _{\varphi(p)} g) . }$ Hence there is a unique ${ A \in L _{\text{is}} (T _p M, T _{\varphi(p)} V) }$ such that ${ (T _{\varphi(p)} g ) \circ A = i _{T _p M}, }$ where ${ i _{T _p M} }$ is the canonical inclusion of ${ T _p M }$ into ${ T _p \mathbb{R} ^n . }$
In other words, ${ A }$ is the inverse of ${ T _{\varphi(p)} g ,}$ when ${ T _{\varphi(p)} g }$ is understood as a map from ${ T _{\varphi(p)} V }$ onto its image ${ T _p M . }$ We call ${ T _p \varphi := A }$ the tangential of the chart ${ \varphi }$ at the point ${ p . }$ Further ${ (T _p \varphi) v \in T _{\varphi(p)} V }$ is called the representation of tangential vector ${ v \in T _p M }$ in the local coordinates induced by ${ \varphi . }$
Let ${ (\tilde{\varphi}, \tilde{U}) }$ be another chart of ${ M }$ near ${ p . }$ Then we have the commutative diagram of isomorphisms

Pf: WLOG assume ${ U = \tilde{U} . }$ Since ${ \tilde{g} = i _M \circ \tilde{\varphi} ^{-1} ,}$ we have ${ \tilde{g} = (i _M \circ \varphi ^{-1} ) \circ (\varphi \circ \tilde{\varphi} ^{-1}) }$ that is

\[{ \tilde{g} = g \circ (\varphi \circ \tilde{\varphi} ^{-1}). }\]

Applying chain rule we have

\[{ T _{\tilde{\varphi} (p)} \tilde{g} = T _{\varphi(p)} g \, \circ \, T _{\tilde{\varphi}(p)} (\varphi \circ \tilde{\varphi} ^{-1}) . }\]

Taking inverses we have

\[{ T _p \tilde{\varphi} = T _{\tilde{\varphi}(p)} (\varphi \circ \tilde{\varphi} ^{-1}) ^{-1} \, \circ \, T _p \varphi }\]

that is

\[{ T _p \tilde{\varphi} = T _{\varphi(p)} (\tilde{\varphi} \circ \varphi ^{-1}) \, \circ \, T _p \varphi }\]

as needed. ${ \blacksquare }$

Obs [Inner product of tangential vectors in local coordinates]:
Let ${ M }$ be an ${ m }$ dimensional ${ C ^q }$ submanifold of ${ \mathbb{R} ^n , }$ and ${ p \in M , }$ and ${ (\varphi, U) }$ is a chart of ${ M }$ near ${ p }$ with associated parameterisation ${ (g, V) . }$
Let ${ x _0 = \varphi(p) . }$ Now for tangential vectors ${ v, w \in T _p M , }$ their inner product is given by

\[{ \begin{aligned} &\, (v \, \vert \, w ) _p \\ = &\, ((T _{x _0} g )(T _p \varphi) v \, \vert \, (T _{x _0} g)(T _p \varphi) w) _p \\ = &\, \bigg( Dg(x _0) \sum _{j=1} ^{m} v _j e _j \, \bigg\vert \, Dg(x _0) \sum _{k=1} ^{m} w _k e _k \bigg) \\ = &\, \sum _{j, k = 1} ^{m} (Dg(x _0) e _j \, \vert \, Dg(x _0) e _k ) \, v _j w _k \\ = &\, \sum _{j, k = 1} ^{m} (D _j g(x _0) \, \vert \, D _k g(x _0) ) \, v _j w _k . \end{aligned} }\]

Here ${ v _j, w _k }$ are components of local representations of ${ v, w }$ respectively, and the matrix of inner products

\[{ g _{jk} (x _0) = (D _j g(x _0) \, \vert \, D _k g(x _0)) \, \, \text{ for } 1 \leq j, k \leq m }\]

is called first fundamental matrix of ${ M }$ with respect to chart ${ \varphi }$ at point ${ p . }$

Eg [Tangential spaces for graphs]:
Let ${ f : X (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^{\ell} }$ be a ${ C ^q }$ map. Recall ${ M := \text{graph}(f) }$ is an ${ n }$ dimensional ${ C ^q }$ submanifold of ${ \mathbb{R} ^{n + \ell} ,}$ and that ${ g(x) := (x, f(x)) }$ for ${ x \in X }$ is a ${ C ^q }$ parameterisation for ${ M . }$
Let ${ p = (x _0, f(x _0)) \in M . }$ Note the tangential ${ T _{x _0} g }$ is given by

\[{ ( T _{x _0} g ) (v) _{x _0} = (p, (v, Df(x _0) v)) \quad \text{ for } (v) _{x _0} \in T _{x _0} X . }\]

Hence the tangential space ${ T _p M = \text{im}(T _{x _0} g) }$ is given by

\[{ T _p M = \lbrace (p, (v, Df(x _0) v)) : v \in \mathbb{R} ^n \rbrace . }\]

Equivalently ${ T _p M }$ is the graph of ${ Df (x _0) }$ attached to the point ${ p = (x _0, f(x _0)) . }$

Def [Coordinate paths]:
Let ${ M }$ be an ${ m }$ dimensional ${ C ^q }$ submanifold of ${ \mathbb{R} ^n, }$ and ${ p \in M , }$ and ${ (\varphi, U) }$ is a chart of ${ M }$ near ${ p }$ with associated parameterisation ${ (g, V) . }$
Let ${ \varepsilon > 0 }$ be such that ${ \varphi(p) + te _j \in V }$ for ${ t \in (-\varepsilon, \epsilon) }$ and ${ j \in \lbrace 1, \ldots, m \rbrace . }$ Then the path

\[{ \gamma _j (t) := g(\varphi(p) + t e _j) \quad \text{ for } t \in (- \varepsilon, \varepsilon) }\]

is called the ${ j }$th coordinate path through ${ p . }$

Obs [Tangents to coordinate paths form a basis of ${ T_p M }$]:
Let ${ M }$ be an ${ m }$ dimensional ${ C ^q }$ submanifold of ${ \mathbb{R} ^n, }$ and ${ p \in M , }$ and ${ (\varphi, U) }$ is a chart of ${ M }$ near ${ p }$ with associated parameterisation ${ (g, V) . }$
For ${ x _0 = \varphi(p), }$ we have

\[{ T _p M = \text{span} \lbrace (D _1 g (x _0)) _p, \ldots, (D _m g (x _0)) _p \rbrace . }\]

That is, the tangent vectors at ${ p }$ on the coordinate paths form a basis of ${ T _p M . }$
Pf: Note that ${ T _p M = \lbrace p \rbrace \times \text{im}(Dg(x _0)) }$ is an ${ m }$ dimensional subspace of ${ T _p \mathbb{R} ^n ,}$ and the columns of ${ Dg(x _0) }$ are given by

\[{ D _j g(x _0) = Dg(x _0) e _j = \dot{\gamma _j } (0) . }\]

Hence we are done. ${ \blacksquare }$

Thm [${ T_p M }$ is the space of path tangents]:
Let ${ M }$ be an ${ m }$ dimensional ${ C ^q }$ submanifold of ${ \mathbb{R} ^n, }$ and ${ p \in M , }$ and ${ (\varphi, U) }$ is a chart of ${ M }$ near ${ p }$ with associated parameterisation ${ (g, V) . }$
Then

\[{ \begin{aligned} &\, T _p M \\ = &\, \left\lbrace (v) _p \in T _p \mathbb{R} ^n : \, \, {\begin{aligned} &\, \exists \varepsilon > 0 \quad \exists \gamma \in C ^1 ((-\varepsilon, \varepsilon), \mathbb{R} ^n) \, \text{ such that} \\ &\, \text{im}(\gamma) \subseteq M, \, \, \gamma(0) = p, \, \, \dot{\gamma}(0) = v \end{aligned}} \right\rbrace . \end{aligned} }\]

Pf: ${ \underline{\subseteq } }$: Let ${ (v) _p \in T _p M }$ and ${ x _0 = \varphi (p) . }$ By definition there exist local coordinates ${ \xi \in \mathbb{R} ^m }$ such that

\[{ v = Dg(x _0) \xi . }\]

Since ${ V = \varphi(U) }$ is open in ${ \mathbb{R} ^m }$ there exists an ${ \varepsilon > 0 }$ such that ${ x _0 + t \xi \in V }$ for ${ t \in (-\varepsilon, \varepsilon) . }$
Now the curve

\[{ \gamma(t) = g(x _0 + t \xi) \quad \text{ for } t \in (-\varepsilon, \varepsilon) }\]

satisfies the required constraints ${ \text{im}(\gamma) \subseteq M , }$ ${ \gamma(0) = p ,}$ and ${ \dot{\gamma}(0) = Dg(x _0) \xi = v . }$

${ \supseteq }$: Suppose ${ \gamma \in C ^1 ((-\varepsilon, \varepsilon), \mathbb{R} ^n) }$ with ${ \text{im}(\gamma) \subseteq M }$ and ${ \gamma(0) = p . }$ Since ${ g }$ is an immersion there exist open sets ${ (x _0, 0) \in \tilde{V} }$ and ${ \tilde{U} }$ in ${ \mathbb{R} ^n }$ and a ${ C ^q }$ isomorphism ${ \psi : \tilde{V} \to \tilde{U} }$ such that

\[{ g(x) = \psi(x, 0) \quad \text{ for } (x, 0) \in \tilde{V} . }\]

By shrinking ${ \varepsilon ,}$ we can assume that ${ \text{im}(\gamma) \subseteq U \cap \tilde{U} . }$ Now

\[{ \gamma(t) = (g \circ \varphi \circ \gamma) (t) = (g \circ \text{pr} _{\mathbb{R} ^m} \circ \psi ^{-1} \circ \gamma) (t) }\]

and from chain rule

\[{ \dot{\gamma}(0) = Dg(x _0) (\text{pr} _{\mathbb{R} ^m} \circ \psi ^{-1} \circ \gamma) ^{\cdot} (0) . }\]

For ${ \xi := (\text{pr} _{\mathbb{R} ^m} \circ \psi ^{-1} \circ \gamma) ^{\cdot} (0) }$ and ${ v := Dg(x _0) \xi, }$ we have ${ (v) _p \in T _p M }$ as needed. ${ \blacksquare }$

Thm [Tangential spaces for regular fibers]:
Let ${ f : X (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^{\ell} }$ be a ${ C ^q }$ map, and ${ c \in \text{im}(f) }$ be a regular value of ${ f . }$ We already saw ${ M := f ^{-1} (c) }$ is an ${ (n - \ell) }$ dimensional ${ C ^q }$ submanifold of ${ \mathbb{R} ^n . }$
Then for ${ p \in M, }$ the tangential space

\[{ T _p M = \ker(T _p f) . }\]

Pf: ${ \subseteq }$: Suppose ${ (v) _p \in T _p M . }$ By previous theorem there is an ${ \varepsilon > 0 }$ and a path ${ \gamma \in C ^1 ((-\varepsilon, \varepsilon), \mathbb{R} ^n) }$ such that ${ \text{im}(\gamma) \subseteq M, }$ ${ \gamma(0) = p , }$ and ${ \dot{\gamma}(0) = v . }$ In particular

\[{ f(\gamma(t)) = c \quad \text{ for all } t \in (-\varepsilon, \varepsilon), }\]

and differentiating this relation we have

\[{ Df(\gamma(0)) \dot{\gamma}(0) = Df(p) v = 0 . }\]

So ${ T _p M \subseteq \ker(T _p f ) . }$

${ \supseteq }$: Since ${ p }$ is a regular point of ${ f , }$ we have

\[{ \dim(\text{im}(T _p f )) = \text{rk}(Df(p)) = \ell }\]

and so by rank formula

\[{ \dim(\ker(T _p f)) = n - \ell. }\]

But the subspace ${ T _p M \subseteq \ker(T _p f ) }$ also has dimension ${ \dim(T _p M) = n - \ell , }$ hence

\[{ T _p M = \ker(T _p f) }\]

as needed. ${ \blacksquare }$

Def [Differentiable maps ${ f : M \to N }$]:
Let ${ M }$ be a ${ C ^q }$ submanifold of ${ \mathbb{R} ^n ,}$ and ${ N }$ be a ${ C ^r }$ submanifold of ${ \mathbb{R} ^{\ell} ,}$ and ${ 1 \leq s \leq \min \lbrace q, r \rbrace . }$
Let ${ f \in C(M, N) , }$ and ${ p \in M , }$ and ${ (\varphi, U) }$ be a chart of ${ M }$ near ${ p , }$ and ${ (\psi, W) }$ be a chart of ${ N }$ near ${ f(p). }$
Now ${ U \cap f ^{-1} (W) }$ is an open neighbourhood of ${ p }$ in ${ M ,}$ so we can assume WLOG that ${ f(U) \subseteq W . }$
We say ${ f }$ is ${ s }$ times continuously differentiable at ${ p }$ if the map

\[{ f _{\varphi, \psi} = \psi \circ f \circ \varphi ^{-1} : \varphi(U) \longrightarrow \psi(W) }\]

is ${ s }$ times continuously differentiable.

Informally, the map ${ f _{\varphi, \psi} }$ just sends coordinates of inputs (near ${ p}$) wrt chart ${ \varphi }$ to coordinates of outputs (near ${ f(p) }$) wrt chart ${ \psi . }$

We will later show the definition is independent of the choice of charts ${ (\varphi, U) }$ and ${ (\psi, W) . }$
We say ${ f \in C(M, N) }$ is ${ s }$ times continuously differentiable if it is ${ s }$ times continuously differentiable at every point in ${ M . }$

Obs [Above definition is independent of the charts]:
Let ${ (\tilde{\varphi}, \tilde{U} ) }$ and ${ (\tilde{\psi}, \tilde{W}) }$ be charts of ${ M }$ around ${ p }$ and ${ N }$ around ${ f(p) }$ respectively, such that ${ f(\tilde{U}) \subseteq \tilde{W} . }$ Then

\[{ f _{\tilde{\varphi}, \tilde{\psi}} = \tilde{\psi} \circ f \circ \tilde{\varphi} ^{-1} = (\tilde{\psi} \circ \psi ^{-1}) \circ f _{\varphi, \psi} \circ (\varphi \circ \tilde{\varphi} ^{-1}) , }\]

hence ${ f _{\tilde{\varphi}, \tilde{\varphi}} }$ is ${ s }$ times continuously differentiable at ${ p }$ if and only if ${ f _{\varphi, \psi} }$ is so.

Obs: If ${ M }$ and ${ N }$ have dimension ${ n }$ and ${ \ell }$ respectively, that is ${ M }$ is open in ${ \mathbb{R} ^n }$ and ${ N }$ is open in ${ \mathbb{R} ^{\ell}, }$ then the above definition agrees with the usual definition of ${ C ^s }$ maps.

Obs [How ${ f : M \to N }$ affects curve velocities]:
Let ${ f : M \to N }$ be ${ C ^1 }$ differentiable at ${ p \in M . }$ Let ${ (\varphi, U) }$ be a chart of ${ M }$ near ${ p }$ and ${ (\psi, W) }$ be a chart of ${ N }$ near ${ f(p), }$ such that ${ f(U) \subseteq W . }$
Let ${ (v) _p \in T _p M . }$ We saw there is a ${ C ^1 }$ curve ${ \gamma }$ lying within ${ M }$ and passing through ${ \gamma(0) = p }$ with velocity ${ \gamma ^{’} (0) = v . }$ Now the image curve ${ f \circ \gamma }$ passes through ${ (f \circ \gamma)(0) = f(p) }$ with velocity ${ (f \circ \gamma) ^{’} (0) . }$ We want to compute this velocity. We have the commutative diagram of mappings

Hence the image curve is given by

\[{ (f \circ \gamma) (t) = (\psi ^{-1} \circ f _{\varphi, \psi} \circ \varphi \circ \gamma )(t). }\]

Since

\[{ g((\varphi \circ \gamma) (t)) = \gamma(t) }\]

we have

\[{ Dg(x _0 ) \, (\varphi \circ \gamma) ^{’} (0) = v }\]

that is ${ (\varphi \circ \gamma) ^{’} (0) }$ are the local coordinates of the tangential vector ${ (v) _p .}$
Now letting ${ h }$ be the parameterisation associated with the chart ${ (\psi, W) , }$ we have

\[{ \begin{aligned} &\, (f \circ \gamma) ^{’} (0) \\ = &\, (h \circ f _{\varphi, \psi} \circ \varphi \circ \gamma) ^{’} (0) \\ = &\, Dh \, (\psi(f(p)) ) \circ Df _{\varphi, \psi} (\varphi (p)) \circ T _p \varphi \, \, v \end{aligned} }\]

that is

\[{ ((f \circ \gamma) ^{’} (0)) _{f(p)} = (T _{f(p)} \psi) ^{-1} \circ T _{\varphi(p)} f _{\varphi, \psi} \circ T _p \varphi \, \, (\gamma ^{’} (0)) _p . }\]

Hence informally the map

\[{ T _p M \longrightarrow T _{f(p)} N , }\] \[{ (v) _p \mapsto (T _{f(p)} \psi) ^{-1} \circ T _{\varphi(p)} f _{\varphi, \psi} \circ T _p \varphi \, \, (v) _p }\]

sends the input velocities ${ ( \gamma ^{’} (0) ) _p }$ to the output velocities ${ ( (f \circ \gamma) ^{’} (0)) _{f(p)} . }$

This suggests the following definition.

Def [Tangential of a map ${ f : M \to N }$]:
Let ${ f : M \to N }$ be ${ C ^1 }$ differentiable at ${ p , }$ and ${ (\psi, W) }$ be a chart of ${ N }$ near ${ f(p) }$ such that ${ f(U) \subseteq W . }$
Recall the local representation ${ f _{\varphi, \psi} }$ of ${ f }$ in the charts ${ \varphi }$ and ${ \psi }$ satisfies that the diagram of mappings

commutes, where ${ \cong }$ means ${ C ^1 }$ diffeomorphic and ${ \overline{n} }$ is the dimension of ${ N . }$

Note that the charts ${ \varphi }$ and ${ \psi }$ are trivially ${ C ^1 }$ diffeomorphisms: They are ${ C ^1 }$ maps because their local representations ${ \varphi _{\varphi, \text{id}} = \text{id} _{\varphi(U)} }$ and ${ \psi _{\psi, \text{id}} = \text{id} _{\psi(W)} }$ are ${ C ^1 }$ maps. Their inverses are ${ C ^1 }$ maps because the local representations ${ (\varphi ^{-1}) _{\text{id}, \varphi} = \text{id} _{\varphi(U)} }$ and ${ (\psi ^{-1}) _{ \text{id}, \psi} = \text{id} _{\psi(W)} }$ are ${ C ^1 }$ maps.

The tangential ${ T _p f }$ of ${ f }$ at ${ p }$ is defined similarly such that the following diagram of mappings

commutes, that is

\[{ T _p f = ( T _{f(p)} \psi ) ^{-1} \circ (T _{\varphi(p)} f _{\varphi, \psi} ) \circ T _p \varphi . }\]

Informally, the definition says the tangential of ${ f }$ is same as the tangential of ${ f _{\varphi, \psi} }$ upto identification of tangential vectors with their local coordinates.

Obs [Above definition is independent of the charts]:
Suppose ${ (\tilde{\varphi}, \tilde{U}) }$ is a chart of ${ M }$ near ${ p }$ and ${ (\tilde{\psi}, \tilde{W}) }$ is a chart of ${ N }$ near ${ f(p) }$ such that ${ f(\tilde{U}) \subseteq \tilde{W} . }$
We are to show

\[{ \text{To show: } \quad {\begin{aligned} &\, (T _{f(p)} \tilde{\psi}) ^{-1} \circ T _{\tilde{\varphi}(p)} f _{\tilde{\varphi}, \tilde{\psi}} \circ T _p \tilde{\varphi} \\ = &\, (T _{f(p)} \psi) ^{-1} \circ T _{\varphi(p)} f _{\varphi, \psi} \circ T _p \varphi \end{aligned}} }\]

We already saw the local representations

\[{ f _{\tilde{\varphi}, \tilde{\psi}} = (\tilde{\psi} \circ \psi ^{-1}) \circ f _{\varphi, \psi} \circ (\varphi \circ \tilde{\varphi} ^{-1}) , }\]

so taking tangentials

\[{ T _{\tilde{\varphi}(p) } f _{\tilde{\varphi}, \tilde{\psi}} = T _{\psi(f(p))} (\tilde{\psi} \circ \psi ^{-1}) \circ T _{\varphi(p)} f _{\varphi, \psi} \circ T _{\tilde{\varphi}(p)} (\varphi \circ \tilde{\varphi} ^{-1}) . }\]

Hence

\[{ T _{\tilde{\varphi}(p) } f _{\tilde{\varphi}, \tilde{\psi}} = T _{f(p)} \tilde{\psi} \circ (T _{f(p)} \psi) ^{-1} \circ T _{\varphi(p)} f _{\varphi, \psi} \circ T _p \varphi \circ (T _p \tilde{\varphi}) ^{-1} }\]

as needed. ${ \blacksquare }$

Obs [Chain rule]:
Consider manifolds ${ M, N, O .}$ Let ${ f : M \to N }$ be ${ C ^1 }$ differentiable at ${ p , }$ and ${ g : N \to O }$ be ${ C ^1 }$ differentiable at ${ f(p) . }$
Then ${ g \circ f }$ is ${ C ^1 }$ differentiable at ${ p }$ with

\[{ T _p (g \circ f) = T _{f(p)} g \circ T _p f . }\]

Pf: Consider charts ${ (\varphi _1, U _1) , }$ ${ (\varphi _2, U _2) }$ and ${ (\varphi _3, U _3) }$ near ${ p, }$ ${ f(p), }$ and ${ g(f(p)) }$ respectively, and WLOG ${ f(U _1) \subseteq U _2 }$ and ${ g(U _2) \subseteq U _3 . }$
Note that we have the commutative diagram of mappings

Hence the tangential

\[{ \begin{aligned} &\, T _p (g \circ f) \\ = &\, (T _{(g \circ f)(p)} \varphi _3 ) ^{-1} \circ T _{\varphi _1 (p)} (g \circ f) _{\varphi _1, \varphi _3} \circ T _p \varphi _1 \\ = &\, (T _{(g \circ f)(p)} \varphi _3 ) ^{-1} \circ T _{\varphi _2 (f(p))} g _{\varphi _2, \varphi _3} \circ T _{\varphi _1 (p)} f _{\varphi _1, \varphi _2} \circ T _p \varphi _1 \\ = &\, (T _{(g \circ f)(p)} \varphi _3 ) ^{-1} \circ T _{\varphi _2 (f(p))} g _{\varphi _2, \varphi _3} \circ T _{f(p)} \varphi _2 \\ &\circ (T _{f(p)} \varphi _2) ^{-1} \circ T _{\varphi _1 (p)} f _{\varphi _1, \varphi _2} \circ T _p \varphi _1 \\ = &\, T _{f(p)} g \circ T _p f \end{aligned} }\]

that is

\[{ T _p (g \circ f) = T _{f(p)} g \circ T _p f }\]

as needed. ${ \blacksquare }$

Obs [Tangential of the inclusion map]:
The canonical inclusion

\[{ i _M : M \longrightarrow \mathbb{R} ^n , \quad x \mapsto x }\]

is a ${ C ^q }$ map, with tangential

\[{ T _p i _M : T _p M \longrightarrow T _p \mathbb{R} ^n, \quad (v) _p \mapsto (v) _p . }\]

Pf: The local representation

\[{ (i _M) _{\varphi, \text{id}} = i _M \circ \varphi ^{-1} = g }\]

is a ${ C ^q }$ map, with tangential

\[{ T _{\varphi(p)} (i _M) _{\varphi, \text{id}} = T _{\varphi(p)} g . }\]

Hence ${ i _M }$ is a ${ C ^q }$ map and with tangential ${ T _p i _M \, \, (v) _p }$ ${ = T _{\varphi(p)} (i _M) _{\varphi, \text{id}} \circ T _p \varphi \, \, (v) _p }$ ${ = (v) _p , }$ as needed. ${ \blacksquare }$

Obs [Restrictions of ${ C ^s }$ maps ${ \tilde{f} : X (\subseteq \mathbb{R} ^n) \to \mathbb{R} ^{\ell} }$ to manifold maps ${ M \to N }$]:
Let ${ M }$ be a ${ C ^q }$ submanifold of ${ \mathbb{R} ^n ,}$ and ${ N }$ be a ${ C ^r }$ submanifold of ${ \mathbb{R} ^{\ell} ,}$ and ${ 1 \leq s \leq \min \lbrace q, r \rbrace . }$
Let ${ X }$ be an open neighbourhood of ${ M ,}$ and ${ \tilde{f} \in C ^s (X, \mathbb{R} ^{\ell}) , }$ and ${ \tilde{f}(M) \subseteq N . }$
Then ${ f = \tilde{f} \vert _M }$ belongs to ${ C ^s (M, N). }$ Now by the commutative diagram of ${ C ^s }$ mappings

we have that the tangentials ${ T _p \tilde{f} }$ and ${ T _p f }$ are related as

\[{ T _{f(p)} i _N \circ T _p f = T _p \tilde{f} \circ T _p i _M \quad \text{ for } p \in M . }\]

Pf: It suffices to show that ${ f = \tilde{f} \vert _M }$ belongs to ${ C ^s (M, N) . }$ Let ${ p \in M . }$ By the definition of a manifold, we see there is an open neighbourhood ${ \tilde{W} }$ of ${ W }$ in ${ \mathbb{R} ^{\ell}, }$ and a ${ C ^r }$ diffeomorphism ${ \Psi }$ of ${ \tilde{W} }$ onto an open subset of ${ \mathbb{R} ^{\ell} ,}$ such that the diffeomorphism ${ \Psi }$ extends the chart ${ \psi . }$ Now note the local representation

\[{ f _{\varphi, \psi} = \psi \circ f \circ \varphi ^{-1} = \Psi \circ \tilde{f} \circ g }\]

belongs to ${ C ^s (V, \mathbb{R} ^{\ell} ) , }$ as needed. ${ \blacksquare }$

Def [Gradient of a map ${ \mathbb{R} ^n \to \mathbb{R} }$ wrt an inner product]:
Let ${ f : X (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} }$ be a ${ C ^1 }$ map and ${ x _0 \in X . }$ Let ${ G = [g _{jk}] \in \mathbb{R} ^{n \times n} }$ be a (symmetric) positive definite matrix. Hence

\[{ (x \, \vert \, y) ^g = x ^T G y }\]

that is

\[{ (x \, \vert \, y) ^g = \sum _{j, k = 1} ^n g _{jk} x _j y _k }\]

defines an inner product on ${ \mathbb{R} ^n . }$
Now there is a unique ${ y \in \mathbb{R} ^n }$ such that

\[{ Df(x _0) \, h = (y \, \vert \, h) ^g \quad \text{ for all } h \in \mathbb{R} ^n . }\]

Note that it is ${ y = (Df(x _0) \, G ^{-1}) ^T }$. We call this the gradient of ${ f }$ at ${ x _0 }$ wrt the inner product ${ ( \cdot \, \vert \, \cdot) ^g , }$ and denote it by ${ \nabla ^g f (x _0) . }$

Def [Gradient of a map ${ f : M \to \mathbb{R} }$]:
Let ${ f : M \to \mathbb{R} }$ be ${ C ^1 }$ differentiable at ${ p \in M . }$ Note the tangential is a map

\[{ T _p f : T _p M \longrightarrow T _{f(p)} \mathbb{R} = \lbrace f(p) \rbrace \times \mathbb{R}, }\]

and we call the second component

\[{ d _p f = \text{pr} _2 \circ T _p f \in L(T _p M, \mathbb{R}) }\]

the differential of ${ f }$ at the point ${ p . }$
Now there is a unique tangential vector ${ \nabla _p ^M f \in T _p M }$ such that

\[{ (d _p f) \, v = ( \nabla _p ^M f \, \vert \, v) _p \quad \text{ for all } v \in T _p M }\]

and we call this the gradient of ${ f }$ at the point ${ p . }$

Obs: Let ${ f : X (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} }$ be a ${ C ^1 }$ map and ${ p \in X . }$ Now

\[{ \nabla _p f = (p, \nabla f(p)) . }\]

Pf: Note the tangential of ${ f }$ is given by

\[{ T _p f \, \, (v) _p = ( Df(p) \, v) _{f(p)} }\]

that is

\[{ d _p f \, \, (v) _p = Df(p) \, v . }\]

Now by the definitions of gradients

\[{ \nabla f(p) = Df(p) ^T \quad \text{ and } \quad \nabla _p f = ( Df(p) ^T) _p }\]

as needed. ${ \blacksquare }$

Obs [Gradient of a map in local coordinates]:
Let ${ f : M \to \mathbb{R} }$ be a ${ C ^1 }$ map and ${ p \in M. }$ As usual let ${ (\varphi, U) }$ be a chart of ${ M }$ near ${ p , }$ and ${ x _0 = \varphi(p) , }$ and ${ f _{\varphi } }$ be the local representation ${ f _{\varphi, \text{id} _{\mathbb{R}} } }$ of ${ f ,}$ and ${ [g _{jk} (x _0) ] }$ be the fundamental matrix with respect to ${ \varphi }$ at the point ${ p }$ with inverse ${ [g ^{jk} (x _0) ] . }$
Then the local representation ${ (T _p \varphi) \nabla _p f }$ of the gradient ${ \nabla _p f \in T _p M }$ has the tangential part given by

\[{ (T _p \varphi) \nabla _p f = [g ^{jk} (x _0)] \, \nabla f _{\varphi} (x _0) . }\]

Pf: Note the tangential of ${ f }$ is given by

\[{ T _p f \, \, (v) _p = T _{x _0} f _{\varphi} \circ T _p \varphi \, \, (v) _p }\]

that is

\[{ d _p f \, \, (v) _p = \sum _{j=1} ^{m} D _j f _{\varphi} (x _0) \, v _j }\]

where ${ (T _p \varphi) v }$ ${ = \sum _{j=1} ^{m} v _j e _j . }$ Now writing ${ (T _p \varphi) \nabla _p f }$ ${ = \sum _{j=1} ^{m} w _j e _j, }$ we have

\[{ \begin{aligned} &\, d _p f \, \, (v) _p \\ = &\, (\nabla _p f \, \vert \, v ) _p \\ = &\, \sum _{j, k = 1} ^{m} g _{jk} (x _0) \, v _j w _k . \end{aligned} }\]

Comparing both expressions gives that

\[{ D _j f _{\varphi} (x _0) = \sum _{k=1} ^{m} g _{jk} (x _0) \, w _k }\]

that is

\[{ \nabla f _{\varphi} (x _0) = [g _{jk} (x _0)] \left( \sum _{k = 1} ^{m} w _k e _k \right) }\]

that is

\[{ \left( \sum _{k = 1} ^{m} w _k e _k \right) = [g ^{jk} (x _0)] \, \nabla f _{\varphi} (x _0) }\]

as needed. ${ \blacksquare }$

Obs [Gradients are zero at local extrema]:
Let ${ f : M \to \mathbb{R} }$ be a ${ C ^1 }$ map and ${ p \in M }$ be a local extremal point of ${ f . }$ Then the gradient at that point ${ \nabla _p f = 0 . }$
Pf: Note the local representation ${ f _{\varphi} \in C ^1 (V, \mathbb{R}) }$ has a local extremum at ${ x _0 = \varphi(p).}$
Hence for all ${ v \in T _p M }$ we have

\[{ (\nabla _p f \, \vert \, v) _p = (d _p f) \, v = \sum _{j = 1} ^{m} D _j f _{\varphi} (x _0) \, v _j = 0 }\]

as needed. ${ \blacksquare }$

Def [Normal spaces]:
The orthogonal complement of ${ T _p M }$ in ${ T _p \mathbb{R} ^n }$ is called the normal space of ${ M }$ at ${ p }$ and is denoted as

\[{ T _p ^{\perp} M = (T _p M) ^{\perp} . }\]

The vectors in ${ T _p ^{\perp} M }$ are called the normals of ${ M }$ at ${ p ,}$ and

\[{ T ^{\perp} M = \bigcup _{p \in M} T _p ^{\perp} M }\]

is called the normal bundle of ${ M .}$

Thm [Normal spaces for regular fibers]:
Let ${ f : X (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} ^{\ell} }$ be a ${ C ^q }$ map, and ${ c \in \text{im}(f) }$ be a regular value of ${ f . }$ We already saw ${ M := f ^{-1} (c) }$ is an ${ (n - \ell) }$ dimensional ${ C ^q }$ submanifold of ${ \mathbb{R} ^n . }$
Now for ${ p \in M }$ the gradients ${ \lbrace \nabla _p f _1 , \ldots, \nabla _p f _{\ell} \rbrace }$ form a basis of the normal space ${ T _p ^{\perp} M . }$
Pf: Recall that ${ \nabla _p f _{j} = (p, D f _j (p) ^{T} ) . }$ Since ${ Df(p) }$ is surjective, we see the rows ${ \lbrace D f _{1} (p), \ldots, Df _{\ell} (p) \rbrace }$ are linearly independent. Hence the gradients ${ \lbrace \nabla _p f _1, \ldots, \nabla _p f _{\ell} \rbrace }$ are linearly independent in ${ T _p \mathbb{R} ^n . }$
Let ${ v \in T _p M . }$ So there is a curve ${ \gamma \in C ^1 ((-\varepsilon, \varepsilon), \mathbb{R} ^n) }$ such that ${ \text{im}(\gamma) \subseteq M , }$ and ${ \gamma (0) = p , }$ and ${ \gamma ^{’} (0) = v . }$ Now since

\[{ f _j (\gamma(t)) = c _j \quad \text{ for } t \in (-\varepsilon, \varepsilon), }\]

we have

\[{ Df _j (p) \, v = 0 \quad \text{ for all } 1 \leq j \leq \ell }\]

that is

\[{ (\nabla _p f _j \, \vert \, v) _p = 0 \quad \text{ for all } 1 \leq j \leq \ell . }\]

Since this is true for all ${ v \in T _p M , }$ we see ${ \nabla _p f _1, \ldots, \nabla _p f _{\ell} }$ are all in ${ T _p ^{\perp} M . }$ Finally

\[{ \dim(T _p ^{\perp} M) = n - \dim(T _p M) = \ell }\]

and hence ${ \nabla _p f _1, \ldots, \nabla _p f _{\ell} }$ form a basis of ${ T _p ^{\perp} M , }$ as needed. ${ \blacksquare }$

Let ${ F : X (\subseteq \mathbb{R} ^n \text{ open}) \to \mathbb{R} }$ be a ${ C ^1 }$ map.
Let ${ h : X (\subseteq \mathbb{R} ^{n} \text{ open}) \to \mathbb{R} ^{\ell} }$ be a ${ C ^1 }$ map, and ${ 0 \in \text{im}(h) }$ be a regular value of ${ h . }$
We already saw ${ M := h ^{-1} (0) }$ is an ${ (n - \ell) }$ dimensional ${ C ^1 }$ submanifold of ${ \mathbb{R} ^n . }$ Suppose ${ (n - \ell) > 0, }$ so that every point in ${ M }$ has a nontrivial tangential space and normal space.
Now the goal is to study the local extrema of ${ f = F \vert _M . }$

Thm [Lagrange multipliers. Optimizing over regular fibers]:
If ${ p \in M }$ is a local extremum of ${ f , }$ then there exist unique ${ \lambda _1, \ldots, \lambda _{\ell} \in \mathbb{R} }$ such that ${ p }$ is a critical point of

\[{ F - \sum _{j=1} ^{\ell} \lambda _j h _j \in C ^1 (X, \mathbb{R}) }\]

that is

\[{ \nabla F (p) = \sum _{j=1} ^{\ell} \lambda _j \nabla h _j (p) . }\]

Pf: Say ${ p \in M }$ is a local extremum of ${ f . }$ By the previous observation about restrictions of maps, we have ${ f \in C ^1 (M, \mathbb{R}) . }$ Hence ${ \nabla _p f = 0 . }$
Now for ${ (v) _p \in T _p M \subseteq T _p \mathbb{R} ^n , }$ we have

\[{ 0 = (\nabla _p f \, \vert \, v ) _p = d _p f \, \, (v) _p = d _p F \, T _p i _{M} \, \, (v) _p = (\nabla F(p) \, \vert \, v ) . }\]

Hence ${ (\nabla F(p) ) _{p} \in T _p ^{\perp} M , }$ that is there are unique ${ \lambda _1, \ldots, \lambda _{\ell} }$ such that

\[{ (\nabla F(p)) _p = \sum _{j = 1} ^{\ell} \lambda _j (\nabla h _j (p)) _p , }\]

as needed. ${ \blacksquare }$

Eg [Spectral theorem for real symmetric matrices]:
Let ${ A \in \mathbb{R} ^{n \times n} }$ be a real symmetric matrix. We can optimize the quadratic form

\[{ F : \mathbb{R} ^n \longrightarrow \mathbb{R}, \quad x \mapsto (x \, \vert \, Ax) }\]

over various regular fibers.
${ \boxed{1} }$ Firstly, let ${ h _{(1)} (x) := \lVert x \rVert ^2 - 1 . }$ The natural regular fiber ${ M _{(1)} = h _{(1)} ^{-1} (0) = S ^{n-1} }$ is compact, so ${ F \vert _{S ^{n-1}} }$ has a maximal point ${ x _1 \in S ^{n-1} . }$ Now by Lagrange multipliers, there is a unique ${ \lambda _1 \in \mathbb{R} }$ such that

\[{ \nabla F (x _1) = \lambda _1 \nabla h _{(1)} (x _1) }\]

that is

\[{ 2 A x _1 = 2 \lambda _1 x _1 . }\]

Therefore the maximal point ${ x _1 \in S ^{n-1} }$ is an eigenvector with eigenvalue ${ \lambda _1, }$ and at this point

\[{ F(x _1) = (x _1 \, \vert \, A x _1) = (x _1 \, \vert \, \lambda _1 x _1) = \lambda _1 . }\]

${ \boxed{2} }$ Secondly, let ${ h _{(2)} (x) := (\lVert x \rVert ^2 - 1, 2(x _1 \, \vert \, x) ) . }$ The regular fiber ${ M _{(2)} = h _{(2)} ^{-1} (0) = S ^{n-1} \cap \text{span}(x _1) ^{\perp} }$ is compact, so ${ F \vert _{M _{(2)}} }$ has a maximal point ${ x _2 \in M _{(2)} .}$ Now by Lagrange multipliers, there exist unique ${ \lambda _{(2), 1}, \lambda _{(2), 2} \in \mathbb{R} }$ such that

\[{ \nabla F(x _2) = \lambda _{(2), 1} \nabla h _{(2), 1} (x _2) + \lambda _{(2), 2} \nabla h _{(2), 2} (x _2) }\]

that is

\[{ 2A x _2 = 2 \lambda _{(2), 1} x _2 + 2 \lambda _{(2), 2} x _1 . }\]

Taking inner product of this with ${ x _1 , x _2 }$ successively, we see

\[{ \underbrace{ (x _1 \, \vert \, A x _2)} _{= (A x _1 \, \vert \, x _2) = 0} = \lambda _{(2), 2} , \quad \text{ and } \quad (x _2 \, \vert \, A x _2) = \lambda _{(2), 1}. }\]

Therefore the maximal point ${ x _2 \in S ^{n-1} \cap \text{span}(x _1) ^{\perp} }$ is an eigenvector with eigenvalue ${ \lambda _{(2), 1} , }$ and at this point

\[{ F(x _2) = (x _2 \, \vert \, A x _2) = (x _2 \, \vert \, \lambda _{(2), 1} x _2) = \lambda _{(2), 1}. }\]

. . .

${ \boxed{n} }$ Finally, let ${ h _{(n)} (x) := (\lVert x \rVert ^2 - 1, 2 (x _1 \, \vert \, x), \ldots, 2(x _{n-1} \, \vert \, x)) .}$ The regular fiber ${ M _{(n)} }$ ${ = h _{(n)} ^{-1} (0) }$ ${ = S ^{n-1} \cap \text{span}(x _1, \ldots, x _{n-1}) ^{\perp} }$ is compact, so ${ F \vert _{M _{(n)}} }$ has a maximal point ${ x _n \in M _{(n)} . }$ Now by Lagrange multipliers, there exist unique ${ \lambda _{(n), 1}, \ldots, \lambda _{(n), n} \in \mathbb{R} }$ such that

\[{ \nabla F(x _n) = \lambda _{(n), 1} \nabla h _{(n), 1} (x _n) + \ldots + \lambda _{(n), n} \nabla h _{(n), n} (x _n) }\]

that is

\[{ 2A x _n = 2 \lambda _{(n), 1} x _n + 2 \lambda _{(n), 2} x _1 + \ldots + 2 \lambda _{(n), n} x _{n-1}. }\]

Taking inner product of this with ${ x _1, \ldots, x _n }$ successively, we see

\[{ \lambda _{(n), 2} = 0, \quad \ldots \quad \lambda _{(n), n} = 0, \quad \text{and} \quad \lambda _{(n), 1} = (x _n \, \vert \, A x _n). }\]

Therefore the maximal point ${ x _n \in S ^{n-1} \cap \text{span}(x _1, \ldots, x _{n-1}) ^{\perp} }$ is an eigenvector with eigenvalue ${ \lambda _{(n), 1}, }$ and at this point

\[{ F(x _n) = (x _n \, \vert \, A x _n) = (x _n \, \vert \, \lambda _{(n), 1} x _n) = \lambda _{(n), 1} . }\]

Now note that we have successively obtained orthonormal vectors ${ x _1, \ldots, x _n }$ with the properties

\[{ \begin{aligned} &\, A x _1 = \lambda _1 x _1, \\ &\, A x _2 = \lambda _2 x _2 , \\ &\, \quad \quad \vdots \\ &\, A x _n = \lambda _n x _n , \end{aligned} }\]

and that additionally

\[{ \begin{aligned} &\, \lambda _1 = \max \lbrace (x \, \vert \, Ax) : x \in S ^{n-1} \rbrace , \\ &\, \lambda _2 = \max \lbrace (x \, \vert \, Ax) : x \in S ^{n-1} \cap \text{span}(x _1) ^{\perp} \rbrace , \\ &\, \quad \quad \vdots \\ &\, \lambda _n = \max \lbrace (x \, \vert \, Ax) : x \in S ^{n-1} \cap \text{span}(x _1, \ldots, x _{n-1}) ^{\perp} \rbrace , \end{aligned} }\]

as needed. ${ \blacksquare }$