Thm: Let ${ X }$ be a set with ${ \sigma -}$algebra ${ \mathfrak{M} }.$ Let ${ f : X \to [0, \infty] }$ be a measurable map.
Then there exist simple measurable maps ${ 0 \leq s _1 \leq s _2 \leq \ldots (\leq f) }$ with pointwise limit ${ \lim _{n \to \infty} s _n (x) = f(x) }$ for all ${ x \in X }.$

Pf: We can try forming a sequence ${ \varphi _n : [0, \infty] \to [0, \infty] }$ so that functions ${ s _n := \varphi _n \circ f }$ do the job. For this, it suffices to have ${ \varphi _n }$ to be simple, be Borel maps (preimage of open sets are Borel) so that ${ \varphi _n \circ f }$ are measurable, and with ${ 0 \leq \varphi _1 \leq \varphi _2 \leq \ldots }$ and ${ \lim _{n \to \infty} \varphi _n = \text{id} }$ pointwise.
We can construct such ${ \varphi _n }.$ For integer ${ n > 0 }$ and real ${ x \in \mathbb{R} },$ notice ${ \lfloor 2 ^n x \rfloor \leq 2 ^n x < \lfloor 2 ^n x \rfloor + 1 }$ that is ${ \frac{ \lfloor 2 ^n x \rfloor}{2 ^n} \leq x < \frac{\lfloor 2 ^n x \rfloor + 1}{2 ^n} }.$ Especially ${ \left\vert x - \frac{ \lfloor 2 ^n x \rfloor}{2 ^n} \right\vert \leq \frac{1}{2 ^n} \to 0 }$ as ${ n \to \infty }.$ So consider \({ \varphi _n (x) : = \begin{cases} \frac{\lfloor 2 ^n x \rfloor}{2 ^n} &\text{ for } 0 \leq x < n \\ n &\text{ for } n \leq x \end{cases} }.\)

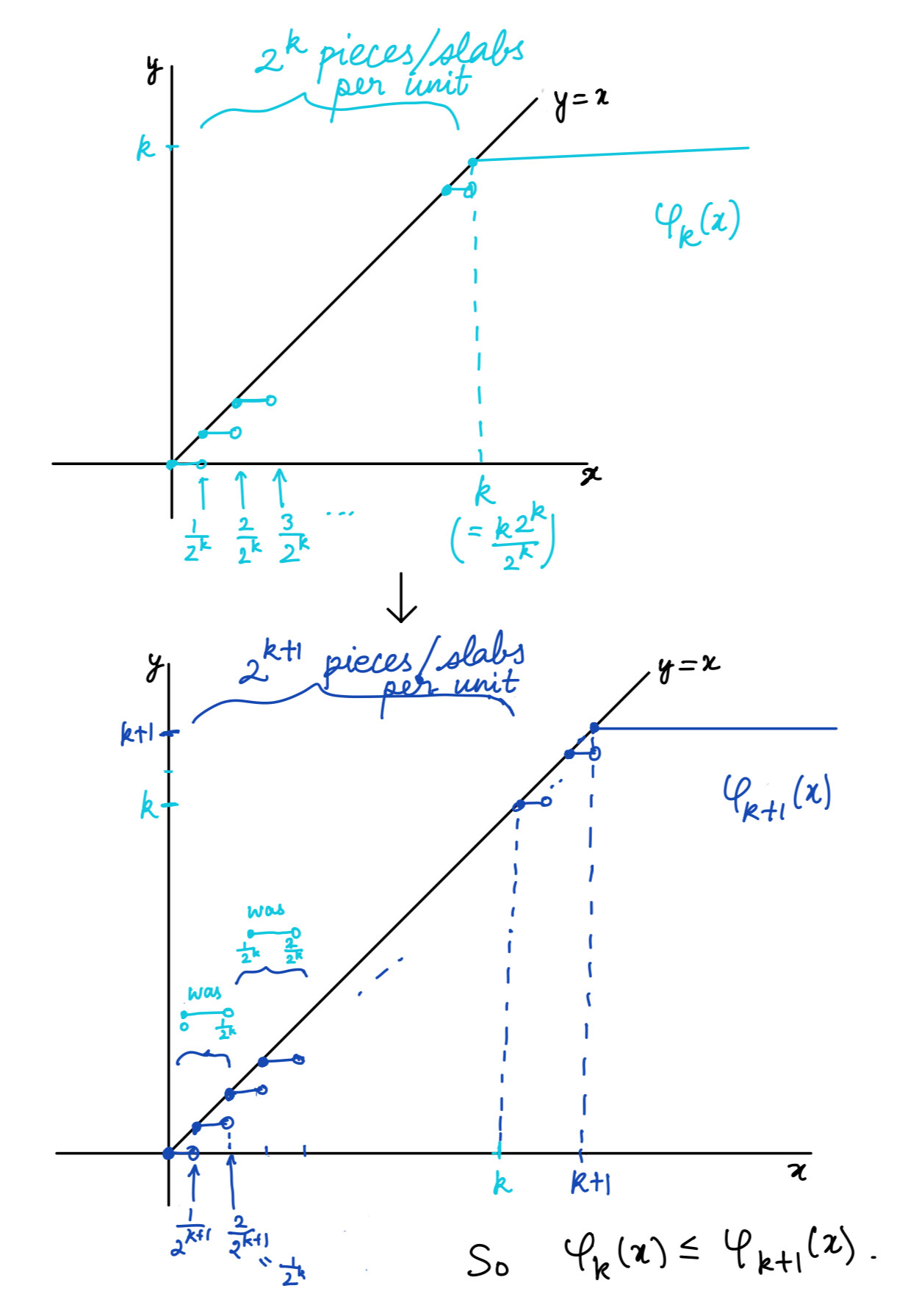
We see these ${ (\varphi _n) }$ satisfy the required properties.